Dự đoán giá cổ phiếu bằng mô hình mạng Echo State Networks

Trong cuốn The West Wing Script Book của Aaron Sorkin, ông ấy đã có một câu như thế này “There (is) order and even great beauty in what looks like total chaos. If we look closely enough at the randomness around us, patterns will start to emerge.”. Mình xin phép không dịch câu nói trên ra, bởi vì mình dịch khá tệ, và câu nói này khá nổi tiếng (đã được trích dẫn khá nhiều trên các bài viết của các bloger khác). Nhưng câu nói đó khá phù hợp với môi trường chứng khoán, nơi mà mọi thứ đều không rõ ràng và khá “hỗn loạn”.

Dự đoán chuỗi thời gian

Giá cổ phiếu trên thị trường chứng khoán thường được quy vào bài toán là time series. Các công ty đầu tư hoặc các nhà nghiên cứu, các nhà đầu tư hiện nay thường sử dụng phương pháp stochastic hoặc các cải tiến của phương pháp stochastic (ví dụ mô hình ARIMA, RegARIMA,…) để đưa ra các dự đoán hợp lý phù hợp với các giá trị quá khứ. Mục tiêu cuối cùng là tìm ra một mô hình khả dĩ nhất để phản ánh quy luật của thị trường và sử dụng nó để sinh ra lợi nhuận (trở nên giàu có hơn :)).

Các thuộc tính của time series

Một trong các thuộc tính của chuỗi thời gian là tính dừng (stationary). Một chuỗi time series được gọi là có tính dừng nếu các thuộc tính có ý nghĩa thống kê của nó (ví dụ như là trung bình, độ lệch chuẩn) không đổi theo thời gian. Ở đây, chúng ta luận bàn nho nhỏ một chút vì sao tính dừng rất quang trọng trong chuỗi thời gian.

Trước hết, hầu hết các mô hình về time series hiện tại được xây dựng trên một giả định tính dừng của chuỗi thời gian. Có nghĩa là nếu chuỗi thời gian ở trong quá khứ có một hành vi nào đó, thì khả năng cao là nó sẽ lặp lại trong tương lai. Ngoài ra, các lý thuyết liên quan đến tính dừng của chuỗi time series đã được các nhà nghiên cứu khai thác một cách triệt để và dễ ràng implement hơn là các lý thuyết về non-stationary trong time series.

Tính dừng được định nghĩa bằng các tiêu chí rõ ràng và nghiêm ngặt. Tuy nhiên, trong bài toán thực tế, chúng ta có thể giả định rằng một chuỗi time series được coi là có tính dừng nếu các thuộc tính thống kê không đổi theo thời gian, nghĩa là:

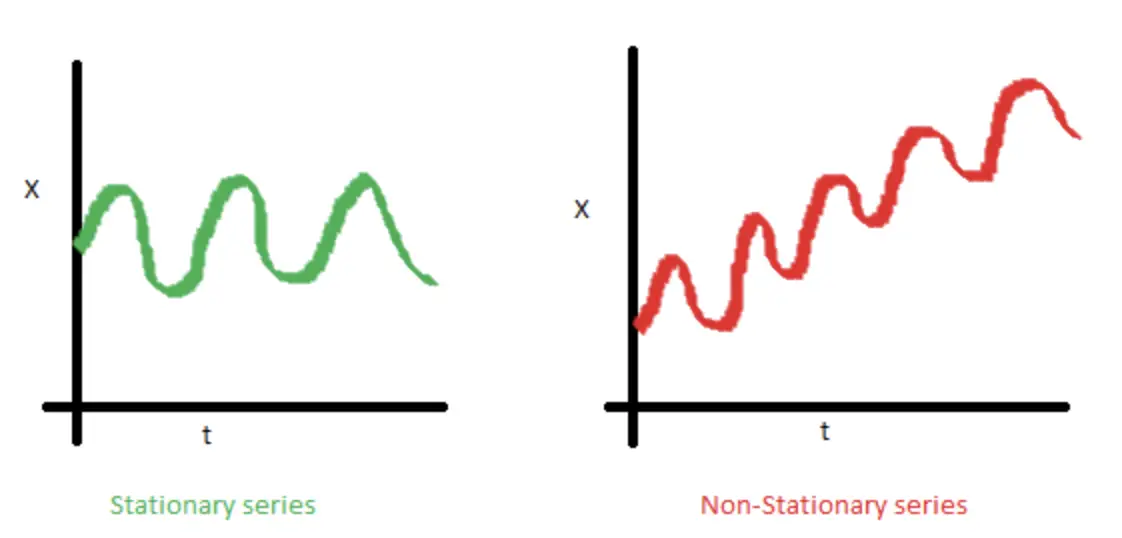
• Giá trị trung bình không thay đổi. Nếu giá trị trung bình thay đổi, chuỗi thời gian sẽ có khuynh hướng đi lên hoặc đi xuống. Hình ảnh bên dưới, mô tả trực quan một chuỗi thời gian có tính dừng (trung bình không thay đổi), và một chuỗi thời gian không có tính dừng (trung bình thay đổi).

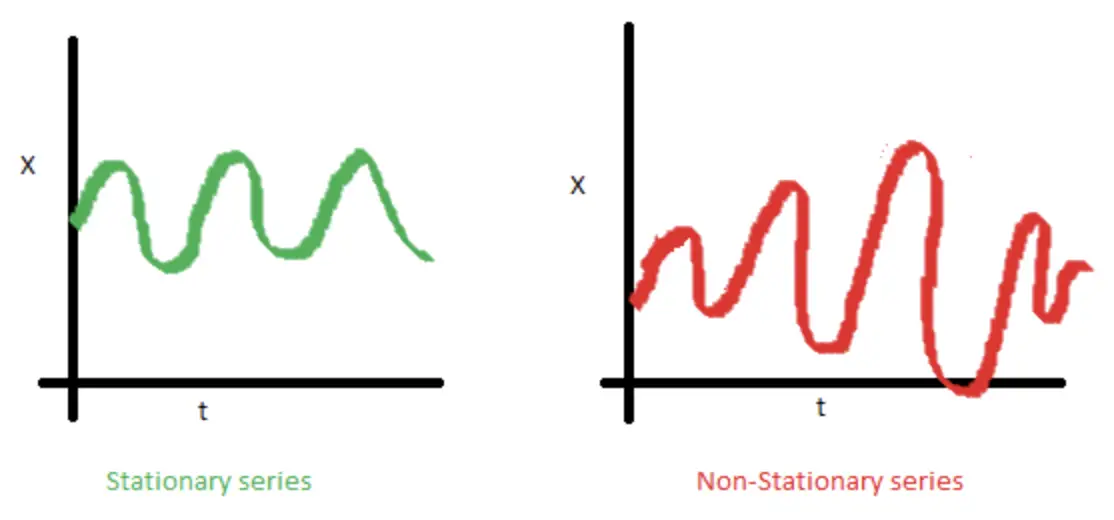
• Giá trị phương sai không thay đổi. Thuộc tính này còn được gọi là đồng đẳng (homoscedasticity). Hình bên dưới mô tả một chuỗi có phương sai thay đổi (không có tính dừng) và một chuỗi có phương sai bất biến (có tính dừng).

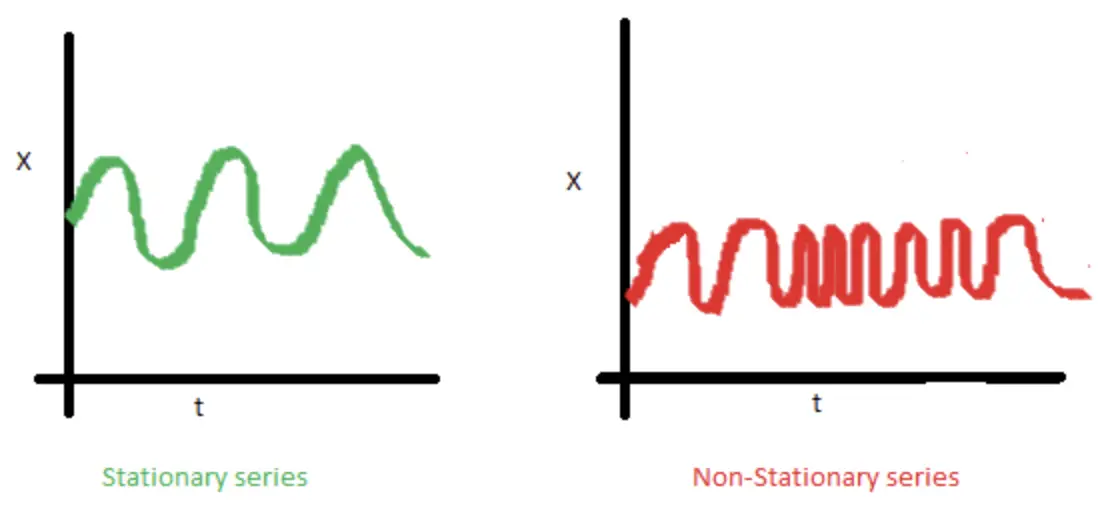
• Tính tự tương tự không phụ thuộc vào thời gian

Vì sao chúng ta lại quan tâm đến tính dừng của dữ liệu

Chúng ta quan tâm đến tính dừng của dữ liệu, đơn giản là bởi vì nếu dữ liệu không có tính dừng, chúng ta không thể xây dựng mô hình chuỗi thời gian (như đã nói ở trên, các nghiên cứu hiện nay đều dựa trên một cơ sở là dữ liệu có tính dừng). Trong trường hợp bạn có trong tay dữ liệu thuộc dạng time series, và một tiêu chí nào đó trong 3 tiêu chí mình đã liệu kê ở trên bị vi phạm, suy ra là dữ liệu của bạn không có tính dừng. Bạn phải chuyển đổi dữ liệu bạn đang có để cho nó có tính dừng. May mắn rằng cũng có nhiều nghiên cứu thực hiện việc này, ví dụ như “khử xu hướng (detrending)”, khử sai biệt (differencing)…

Nếu bạn mới chỉ bắt đầu phân tích chuỗi thời gian, bạn sẽ thấy việc làm trên khá là stupid. Lý thuyết tốt nhất hiện nay cho chuỗi thời gian là chia nhỏ nó ra thành các thành phần như là xu hướng (linear trend), mùa vụ (seasonal), chu kỳ, và yếu tố ngẫu nhiên. Dự đoán cho từng phần một, sau đó lấy tổng chúng lại.

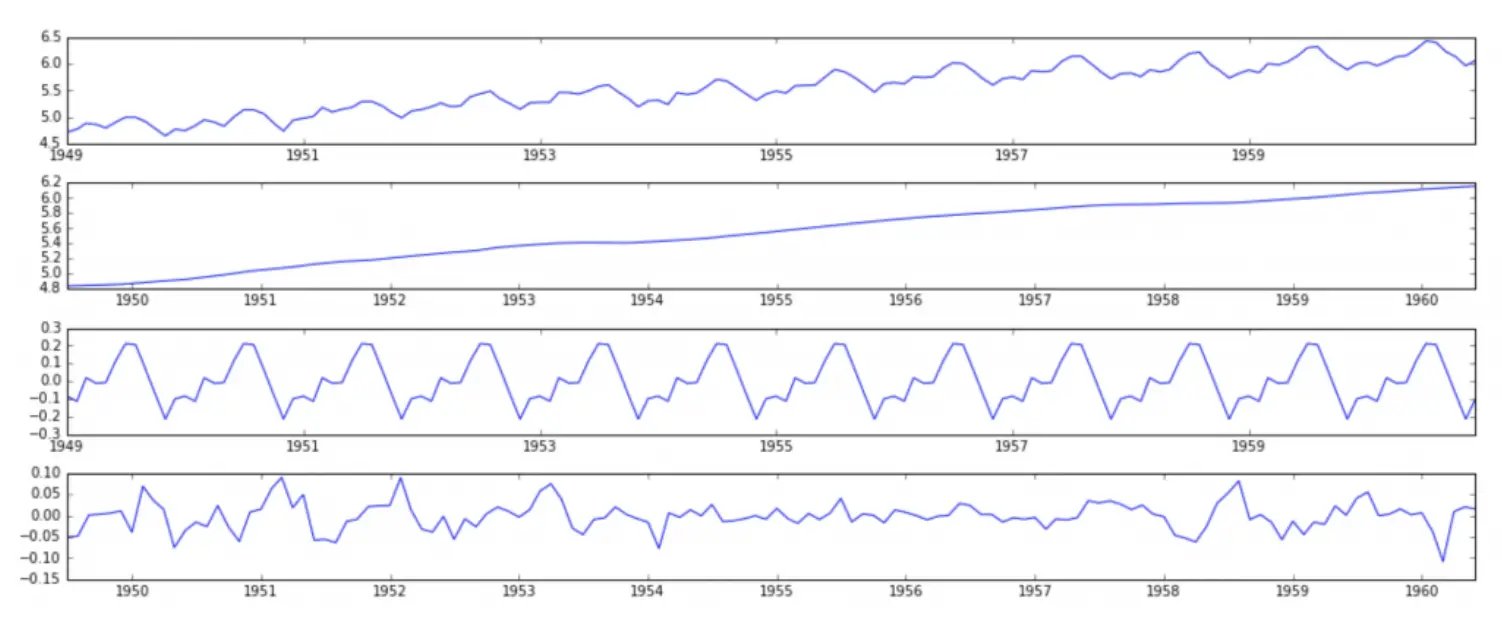
Đối với những ai đã quen thuộc với biến đổi Fourier, thì sẽ dễ dàng “cảm” hơn cái mình vừa nói ở trên.

Cách xác định tính dừng của dữ liệu

Khá khó để xác định một biểu đồ chuỗi time series có tính dừng hay không (quan sát biểu đồ bằng mắt). Cho nên chúng ta sẽ sử dụng kiểm định Dickey-Fuller. Đây là một kiểm định thống kê để kiểm tra xem chuỗi dữ liệu có tính dừng hay không. Với giả thuyết null là chuỗi time series là một chuỗi không có tính dừng. Nếu giá trị nhỏ hơn một ngưỡng p-value nào đó (thường là 0.05), chúng ta có quyền bác bỏ giả định null, và nói rằng chuỗi thời gian đang có là có tính dừng. Ở bài viết này, mình không đề cập đến mô hình kiểm định - vốn được học trong môn xác xuất thống kê. Các bạn có nhu cầu tìm hiểu thì có thể search trên google hoặc là xem lại sách xác suất thống kê.

Phương pháp dự đoán chuỗi thời gian cơ bản

Phương pháp cơ bản nhất, đơn giản nhất, và để áp dụng nhất dược sử dụng để dự đoán chuỗi thời gian là moving average. Mô hình này thực hiện tính trung bình của t giá trị cuối cùng làm giá trị dự đoán của điểm tiếp theo. Ví dụ như để dự đoán giá chứng khoán của ngày thứ 2 của tuần tiếp theo, chúng ta sẽ lấy trung bình giá đóng của của 5 ngày trước đó (giá từ thứ hai đến thứ sáu tuần này).

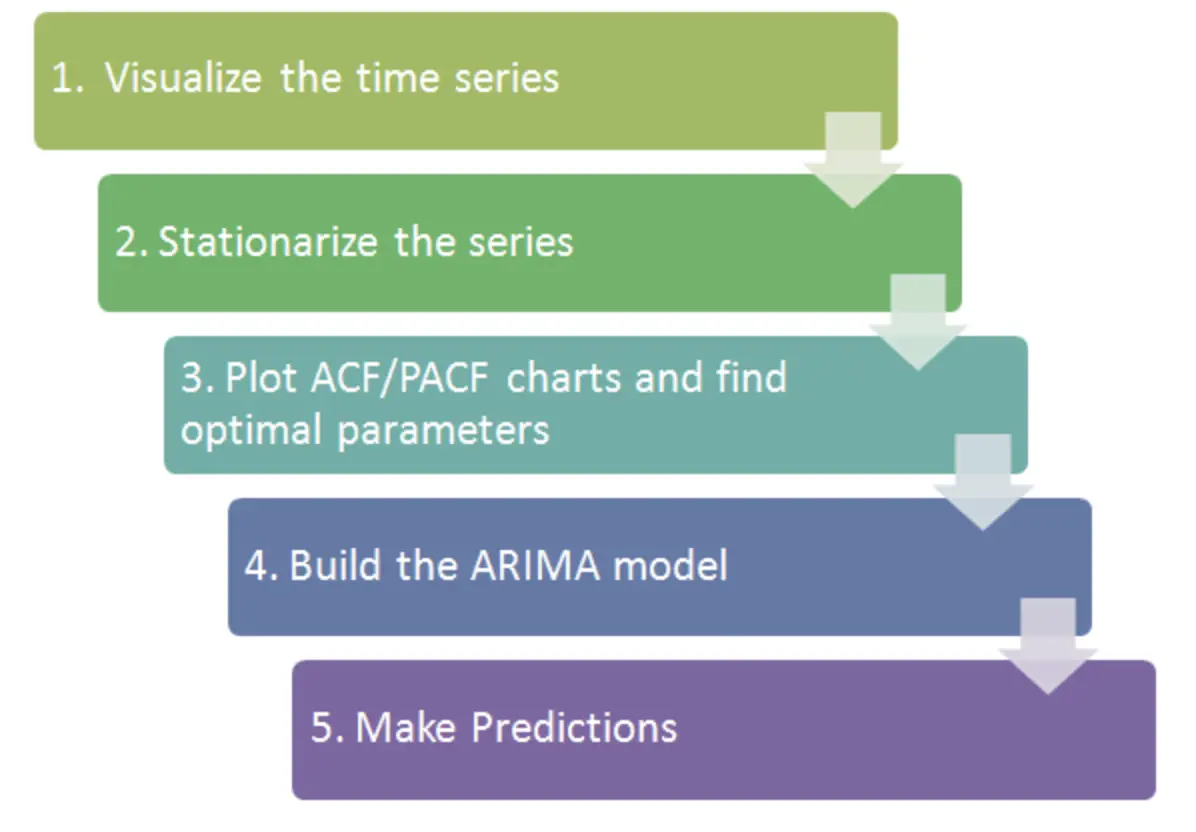
Đến đây, các bạn đã có một số hiểu biết về time series. Một mô hình khá nổi tiếng là ARIMA đã được sử dụng nhiều để phân tích và dự báo. Cách thực hiện của mô hình trên được trình bày tóm gọn trong hình mô tả bên dưới.

Phương pháp dự đoán dựa vào mạng neural network

Thực tế, có rất nhiều mạng neural network đã được áp dụng để dự đoán mô hình chứng khoán. Các bạn có thể tìm đọc lại các bài viết trước đây của mình về sử dụng LSTM trong dự báo chứng khoán. Mô hình chứng khoán bằng mạng neural network nói chung phải đối mặt với một vấn đề khá “xương xẩu” là xử lý nhiễu và vanishing gradients. Trong đó, việc xử lý vanishing gradients là quan trọng nhất. Bản chất của mạng neural network là tối ưu hoá hàm lan truyền ngược bằng cách sử dụng đạo hàm giữa các lớp layer để chúng ‘học’. Trải qua nhiều layer, giá trị của đạo hàm sẽ càng ngày nhỏ dần vào xấp xỉ bằng 0. Giả sử chúng ta có một mô hình có 100 lớp hidden layer, chúng ta nhân 100 lần số 0.1 với nhau và boom, giá trị cuối cùng chung ta nhận được là 0, nghĩa là chúng ta chẳng học được cái gì cả.

May mắn thay, tới thời điểm hiện tại, chúng ta có 3 cách để xử lý vấn đề trên:

• Clipping gradients

• LSTM (Long Short Term Memory) hoặc GRU (Gate Recurrent Units)

• Echo states RNNs

Kỹ thuật clipping gradients sử dụng một mẹo là khi giá trị đạo hàm quá lớn hoặc quá nhỏ, chúng ta sẽ không lấy đạo hàm nữa. Kỹ thuật này thoạt nhìn có vẻ hay, nhưng nó không thể ngăn chúng ta mất mát thông tin và đây là một ý tưởng khá tệ.

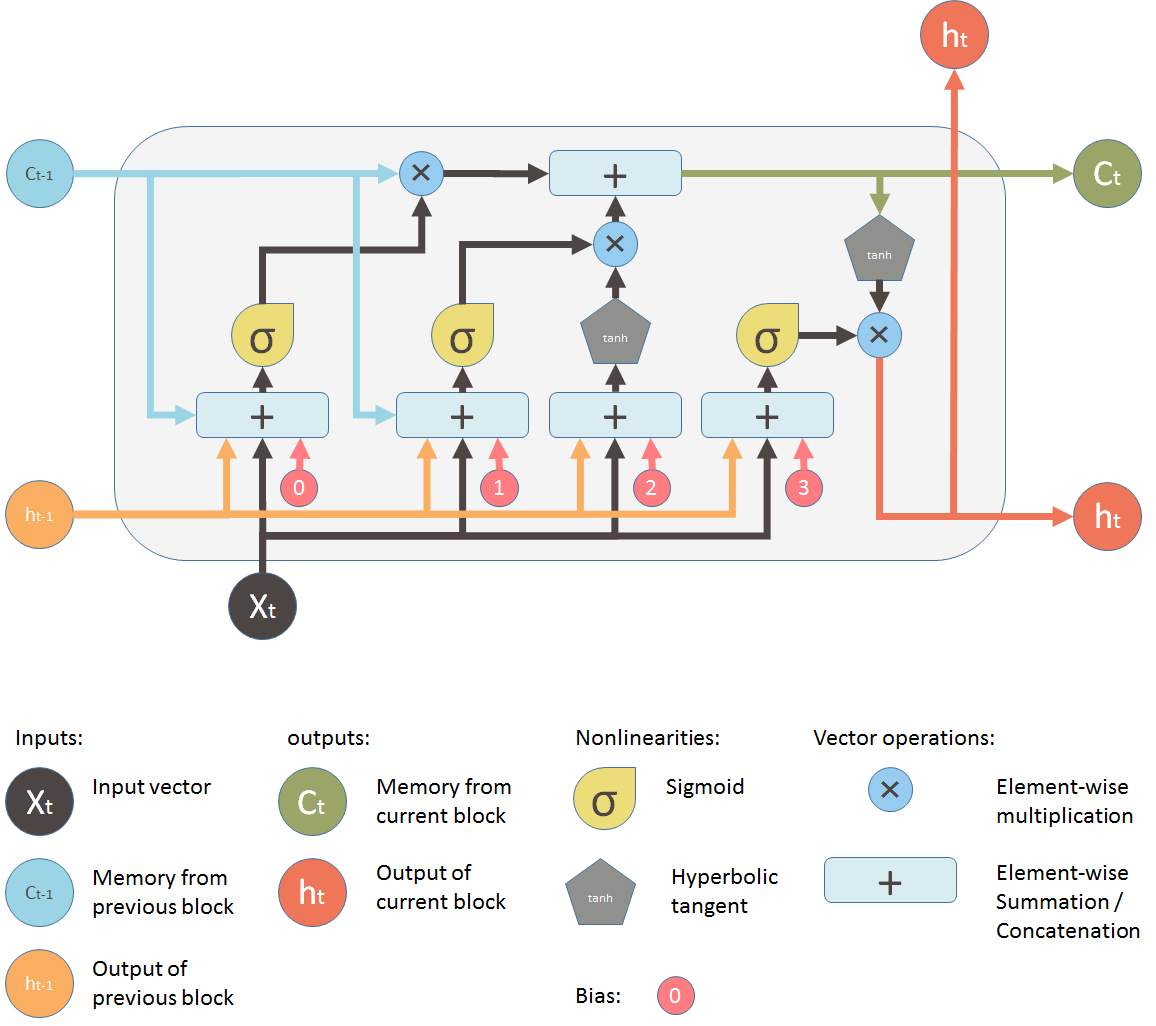
RNN (LSTM hoặc GRU) là một kỹ thuật khác là điều chỉnh các kết nối theo một vài quy luật nhất định, ví dụ output của layer tầng 1 có thể là input của layer tầng 10, chứ không nhất thiết là input của layer tầng 2 như cách thông thường. Kỹ thuật này khá tốt về mặt lý thuyết. Tuy nhiên, có một vấn đề khá lớn khi sử dụng là chúng ta phải tính toán kỹ các kết nối để đảm bảo hệ thống hoạt động ổn đinh. Mô hình được xây dựng trên kỹ thuật này khá bự, làm cho thuật toán chạy chậm. Ngoài ra, tính hội tụ của thuật toán không được đảm bảo. Mô hình LSTM đơn giản mình có để ở hình bên dưới.

Mạng echo states network, là một mô hình mới được nghiên cứu gần đây, bản chất nó là một mảng recurrent neural network với các hidden layer liên kết “lỏng lẻo” với nhau. Lớp này được gọi là ‘reservoir’ (như hình mô tả bên dưới).

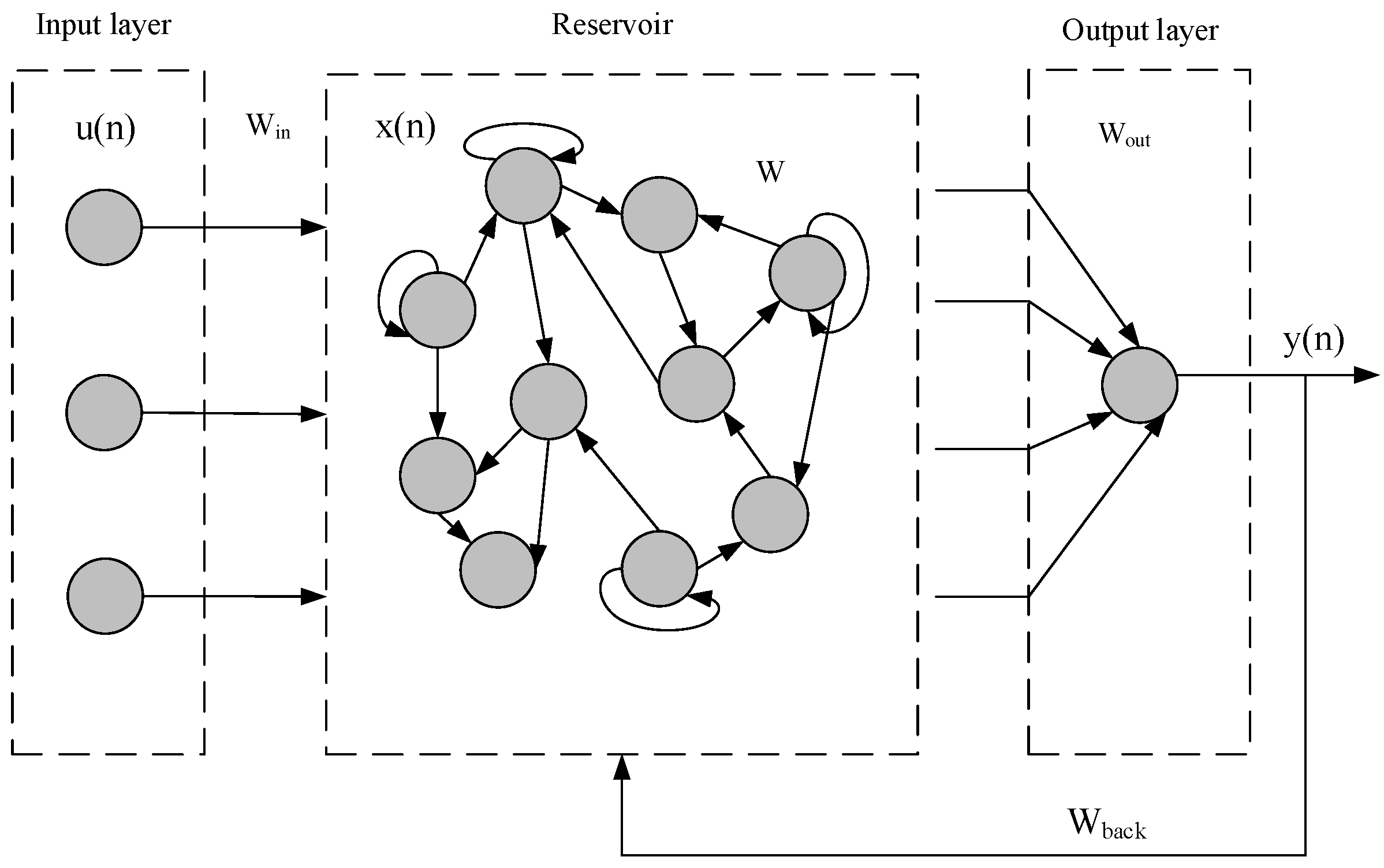
Trong mô hình mạng echo state network, chúng ta chỉ cần huấn luyện lại trọng số của lớp output, việc này giúp chúng ta rút ngắn thời gian huấn luyện mô hình, và tăng tốc qusa trình training.

Sử dụng mạng Echo State Networks

Về nguyên lý hoạt động của mô hình này, mình sẽ không đề cập ở đây. Chủ đề về mạng Echo State Networks mình sẽ nghiên cứu kỹ lưỡng và đề cập ở trong bài viết sắp tới. Mục tiêu của bài viết này là sử dụng mô hình Echo State Networks trong bài toán time series.

Dự doán chuỗi time series

Trước tiên, chúng ta sẽ import một số thư viện cần thiết, thư viện ESN đã có sẵn tại đường dẫn pyESN, các bạn download về rồi dùng

import numpy as np
import pandas as pd
import seaborn as sns
from matplotlib import pyplot as plt
import warnings
warnings.filterwarnings('ignore')

# This is the library for the Reservoir Computing got it by: https://github.com/cknd/pyESN
from pyESN import ESN 

Tiếp theo chúng ta sẽ đọc file

data = open("amazon.txt").read().split()
data = np.array(data).astype('float64')

Chúng ta sẽ xây dựng một mô hình ESN đơn giản

n_reservoir= 500
sparsity=0.2
rand_seed=23
spectral_radius = 1.2
noise = .0005


esn = ESN(n_inputs = 1,
      n_outputs = 1, 
      n_reservoir = n_reservoir,
      sparsity=sparsity,
      random_state=rand_seed,
      spectral_radius = spectral_radius,
      noise=noise)
      
      ```
      
Để đơn giản, mình sẽ tạo mô hình với dữ liệu tào lao như sau:input là một vector toàn số 1, output là các điểm dữ liệu của mình. Cho mô hình ESN học với số lượng phần tử là 1500, sau đó sẽ dự đoán 10 điểm dữ liệu tiếp theo. Với bước nhảy là 10, lặp 10 lần. Sau quá trình lặp, mình thu được 100 điểm dự đoán


```python
trainlen = 1500
future = 10
futureTotal=100
pred_tot=np.zeros(futureTotal)

for i in range(0,futureTotal,future):
    pred_training = esn.fit(np.ones(trainlen),data[i:trainlen+i])  # dữ liệu từ ngày i đến ngày i + trainlen
    prediction = esn.predict(np.ones(future))
    pred_tot[i:i+future] = prediction[:,0] # dự đoán cho ngày i+ trainlen + 1 đến ngày i + trainlen + future
    
    
    ```
    
Vẽ mô hình cùi mía của mình mới làm lên để xem dữ liệu dự đoán và dữ liệu thực tế chênh lệch như thế nào

```python
plt.figure(figsize=(16,8))
plt.plot(range(1000,trainlen+futureTotal),data[1000:trainlen+futureTotal],'b',label="Data", alpha=0.3)
#plt.plot(range(0,trainlen),pred_training,'.g',  alpha=0.3)
plt.plot(range(trainlen,trainlen+futureTotal),pred_tot,'k',  alpha=0.8, label='Free Running ESN')

lo,hi = plt.ylim()
plt.plot([trainlen,trainlen],[lo+np.spacing(1),hi-np.spacing(1)],'k:', linewidth=4)

plt.title(r'Ground Truth and Echo State Network Output', fontsize=25)
plt.xlabel(r'Time (Days)', fontsize=20,labelpad=10)
plt.ylabel(r'Price ($)', fontsize=20,labelpad=10)
plt.legend(fontsize='xx-large', loc='best')
sns.despine()
plt.show()

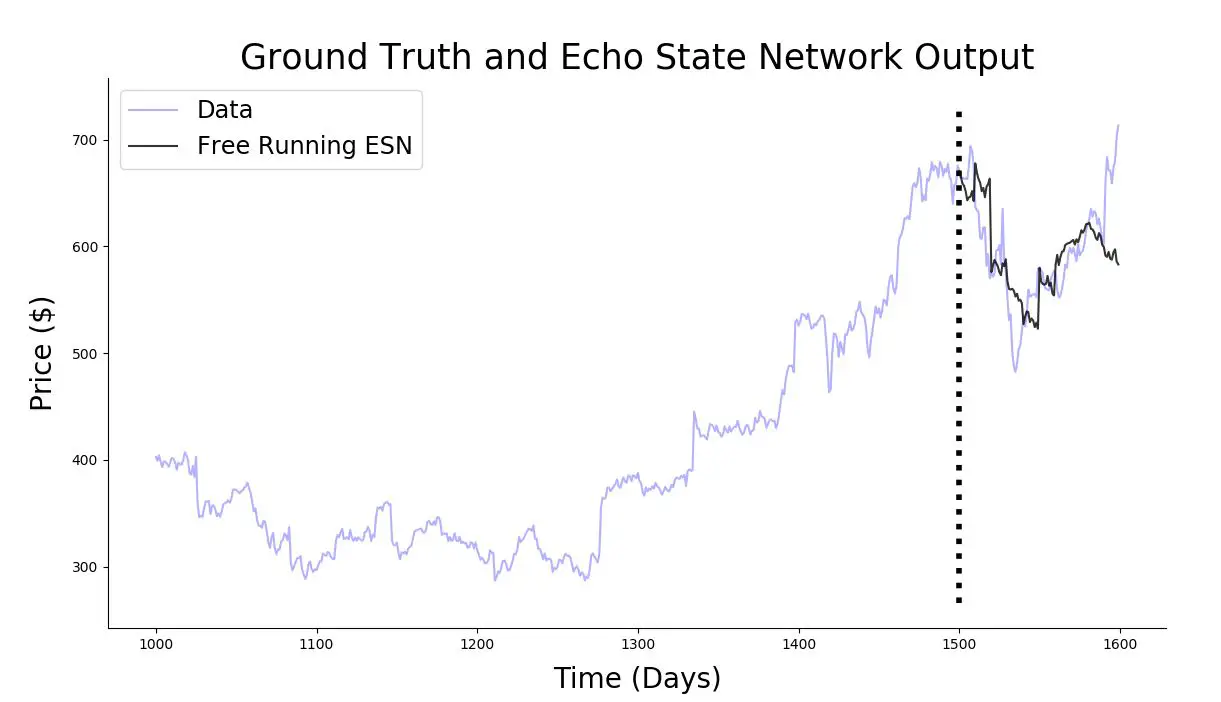
Độ phức tạp của mô hình là khá nhỏ khi so với mô hình RNN. Lý do là về bản chất, chúng ta chỉ huấn luyện trên trọng số của output layer, nó là một hàm tuyến tính. Do vậy, độ phức tạp tính toán chỉ giống như là việc tính một hàm hồi quy tuyến tính. Trong thực tế, độ phức tạp tính toán sẽ là O(N) với N là ố lượng hidden unit trong reservoir.

Tối ưu hoá các tham số Hyper parameters

Ở phần trước, chúng ta set đại các tham số spectral_radius = 1.2 và noise = .0005. Trong thực tế, chúng ta phải tìm các siêu tham số này bằng cách tìm ra mô hình trả về MSE là nhỏ nhất.

Sử dụng kỹ thuật Grid Search với ngưỡng spectrum_radius nằm trong đoạn [0.5, 1.5] và noise nằm trong đoạn noise [0.0001, 0.01], chú ý là các bạn có thể search ở đoạn lớn hơn. Kết quả thu được:

def MSE(yhat, y):
    return np.sqrt(np.mean((yhat.flatten() - y)**2))
    
    n_reservoir= 500
sparsity   = 0.2
rand_seed  = 23
radius_set = [0.9,  1,  1.1]
noise_set = [ 0.001, 0.004, 0.006]

radius_set = [0.5, 0.7, 0.9,  1,  1.1,1.3,1.5]
noise_set = [ 0.0001, 0.0003,0.0007, 0.001, 0.003, 0.005, 0.007,0.01]



radius_set_size  = len(radius_set)
noise_set_size = len(noise_set)

trainlen = 1500
future = 2
futureTotal= 100

loss = np.zeros([radius_set_size, noise_set_size])

for l in range(radius_set_size):
    rho = radius_set[l]
    for j in range(noise_set_size):
        noise = noise_set[j]

        pred_tot=np.zeros(futureTotal)

        esn = ESN(n_inputs = 1,
          n_outputs = 1, 
          n_reservoir = n_reservoir,
          sparsity=sparsity,
          random_state=rand_seed,
          spectral_radius = rho,
          noise=noise)

        for i in range(0,futureTotal,future):
            pred_training = esn.fit(np.ones(trainlen),data[i:trainlen+i])
            prediction = esn.predict(np.ones(future))
            pred_tot[i:i+future] = prediction[:,0]
        
        loss[l, j] = MSE(pred_tot, data[trainlen:trainlen+futureTotal])        
        print('rho = ', radius_set[l], ', noise = ', noise_set[j], ', MSE = ', loss[l][j] )
        

Kết quả

('rho = ', 0.5, ', noise = ', 0.0001, ', MSE = ', 20.367056799629353)
('rho = ', 0.5, ', noise = ', 0.0003, ', MSE = ', 22.44956008062169)
('rho = ', 0.5, ', noise = ', 0.0007, ', MSE = ', 24.574909979223666)
('rho = ', 0.5, ', noise = ', 0.001, ', MSE = ', 25.862558649155638)
('rho = ', 0.5, ', noise = ', 0.003, ', MSE = ', 29.882933676750657)
('rho = ', 0.5, ', noise = ', 0.005, ', MSE = ', 32.63942614291128)
('rho = ', 0.5, ', noise = ', 0.007, ', MSE = ', 36.441245548726)
('rho = ', 0.5, ', noise = ', 0.01, ', MSE = ', 44.77637915282457)
('rho = ', 0.7, ', noise = ', 0.0001, ', MSE = ', 19.560517902720054)
('rho = ', 0.7, ', noise = ', 0.0003, ', MSE = ', 20.12742795009036)
('rho = ', 0.7, ', noise = ', 0.0007, ', MSE = ', 20.81801427735713)
('rho = ', 0.7, ', noise = ', 0.001, ', MSE = ', 21.26142619965559)
('rho = ', 0.7, ', noise = ', 0.003, ', MSE = ', 23.270880660885513)
('rho = ', 0.7, ', noise = ', 0.005, ', MSE = ', 26.061347331527354)
('rho = ', 0.7, ', noise = ', 0.007, ', MSE = ', 30.298361979419834)
('rho = ', 0.7, ', noise = ', 0.01, ', MSE = ', 39.17074955771047)
('rho = ', 0.9, ', noise = ', 0.0001, ', MSE = ', 18.612970860501118)
('rho = ', 0.9, ', noise = ', 0.0003, ', MSE = ', 18.681815816990774)
('rho = ', 0.9, ', noise = ', 0.0007, ', MSE = ', 18.835785386862582)
('rho = ', 0.9, ', noise = ', 0.001, ', MSE = ', 18.982346096338105)
('rho = ', 0.9, ', noise = ', 0.003, ', MSE = ', 20.81632098844061)
('rho = ', 0.9, ', noise = ', 0.005, ', MSE = ', 24.60968377490799)
('rho = ', 0.9, ', noise = ', 0.007, ', MSE = ', 30.231007189936882)
('rho = ', 0.9, ', noise = ', 0.01, ', MSE = ', 41.28587340583505)
('rho = ', 1, ', noise = ', 0.0001, ', MSE = ', 18.23852181110818)
('rho = ', 1, ', noise = ', 0.0003, ', MSE = ', 18.27010615150326)
('rho = ', 1, ', noise = ', 0.0007, ', MSE = ', 18.36078059388596)
('rho = ', 1, ', noise = ', 0.001, ', MSE = ', 18.47920006882226)
('rho = ', 1, ', noise = ', 0.003, ', MSE = ', 20.613227951906246)
('rho = ', 1, ', noise = ', 0.005, ', MSE = ', 25.153712109142973)
('rho = ', 1, ', noise = ', 0.007, ', MSE = ', 31.700838835741898)
('rho = ', 1, ', noise = ', 0.01, ', MSE = ', 44.23736750779224)
('rho = ', 1.1, ', noise = ', 0.0001, ', MSE = ', 17.981571756431556)
('rho = ', 1.1, ', noise = ', 0.0003, ', MSE = ', 18.009398312163942)
('rho = ', 1.1, ', noise = ', 0.0007, ', MSE = ', 18.09054736889828)
('rho = ', 1.1, ', noise = ', 0.001, ', MSE = ', 18.218795249276663)
('rho = ', 1.1, ', noise = ', 0.003, ', MSE = ', 20.82610561349463)
('rho = ', 1.1, ', noise = ', 0.005, ', MSE = ', 26.272452530336505)
('rho = ', 1.1, ', noise = ', 0.007, ', MSE = ', 33.91532767431614)
('rho = ', 1.1, ', noise = ', 0.01, ', MSE = ', 48.22002405965967)
('rho = ', 1.3, ', noise = ', 0.0001, ', MSE = ', 17.72839068197909)
('rho = ', 1.3, ', noise = ', 0.0003, ', MSE = ', 17.799908079894703)
('rho = ', 1.3, ', noise = ', 0.0007, ', MSE = ', 17.92917208443474)
('rho = ', 1.3, ', noise = ', 0.001, ', MSE = ', 18.143905288756557)
('rho = ', 1.3, ', noise = ', 0.003, ', MSE = ', 22.20343747458126)
('rho = ', 1.3, ', noise = ', 0.005, ', MSE = ', 30.05977704513729)
('rho = ', 1.3, ', noise = ', 0.007, ', MSE = ', 40.56654468067572)
('rho = ', 1.3, ', noise = ', 0.01, ', MSE = ', 59.43231026660687)
('rho = ', 1.5, ', noise = ', 0.0001, ', MSE = ', 17.627409489404897)
('rho = ', 1.5, ', noise = ', 0.0003, ', MSE = ', 17.835052829116567)
('rho = ', 1.5, ', noise = ', 0.0007, ', MSE = ', 18.100099619981393)
('rho = ', 1.5, ', noise = ', 0.001, ', MSE = ', 18.481406587483956)
('rho = ', 1.5, ', noise = ', 0.003, ', MSE = ', 24.887601182697498)
('rho = ', 1.5, ', noise = ', 0.005, ', MSE = ', 36.34166374510305)
('rho = ', 1.5, ', noise = ', 0.007, ', MSE = ', 50.99612645577753)
('rho = ', 1.5, ', noise = ', 0.01, ', MSE = ', 75.94229622771246)

Kết quả thu được là giá trị MSE tốt nhất là spectrum radius = 1.5 và nnoise = 0.0001

Thử dự đoán giá cổ phiếu của tập đoàn thế giới di động (Mã cổ phiếu MWG) xem sao

Ở hình trên, mình không tiến hành grid search mà lấy lại các hyper parameters cũ để huấn luyện mô hình. Kết quả như hình trên mình thấy cũng khá tốt rồi, nên mình không tiến hành grid search lại để tìm kết quả tốt hơn.

Dựa vào kết quả chúng ta thu được, có thể nói rằng mô hình ESN dự đoán khá tốt dữ liệu thuộc dạng time series với độ hỗn loạn cao. Đây là một kết luận nhỏ của mình dựa vào bằng chứng trên việc mình test trên tập dữ liệu ngẫu nhiên mà mình có.

Cảm ơn các bạn đã theo dõi. Hẹn gặp bạn ở các bài viết tiếp theo.